增量式学习介绍

发表于 更新于 分类于 ， 阅读次数： 本文字数： 5.5k 阅读时长 ≈ 5 分钟

人工智能的参照样本始终没有离开我们人类自身。终身、增量式地学习能力是人类最重要的特点与能力之一。机器人如果能够像人类一样通过学习来不断地适应新环境与新任务，便有可能实现通用/强人工智能。然而，本文要介绍的增量式学习原本就是领域老人们为了实现类人学习而作的众多尝试之一。

一、增量式学习的基本定义

抛除了类人学习这么大的帽子，增量式学习有它重要的现实意义：

1） 在现实世界中，数据一般是以序列的方式被机器人获取的，这些在线获取的数据包含新的知识需要被机器人学习。因此，机器人的学习系统能够从新获取的数据学习到新的知识。

2）对一个训练好的系统进行修改付出的代价通常低于重新训练一个系统。

增量式学习的思想可以描述为：每当新增数据时，并不需要重建知识库，而是在原有知识库的基础上，仅仅对由于新数据所带来的新信息对知识库进行增量式更新。这种增量式学习的方式使得机器人更加接近人类。现有的增量式学习框架有很多，各种框架的核心内容是：研究更有效的评价新数据与已存储知识相似性的方法。

相似性评价方法决定了觉察新知识与增长知识库的方式，它作为新知识的判定机制是增量式学习的核心部件。下面小节会针对几种常见的增量式学习框架进行介绍，主要包括自组织增量式学习神经网络(SOINN)[1]、情景记忆马尔可规决策过程(EM-MDP)[2]、增量式分级判别回归树(IHDR)[3]。

二、自组织增量式学习神经网络-SOINN

自组织增量学习神经网络SOINN是一种基于竞争学习的两层神经网络。SOINN的增量性使得它能够发现数据流中出现的新模式并进行学习，同时不影响之前学习的结果。因此SOINN能够作为一种通用的学习算法应用于各类非监督学习问题中。
SOINN是两层结构（不包括输入层）的竞争性神经网络，它以自组织的方式对输入数据进行在线聚类和拓扑表示，其工作过程如图1所示。

img

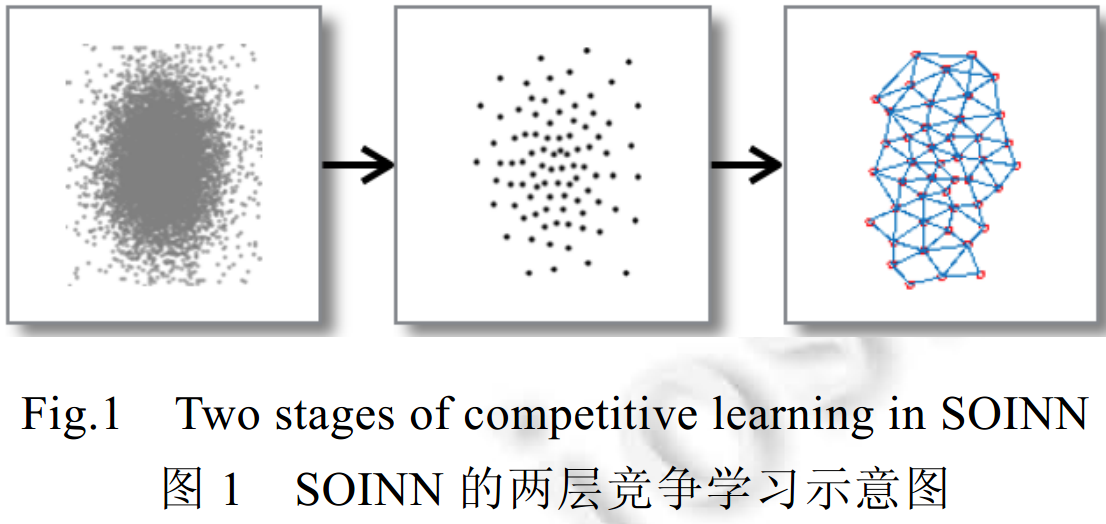
  • 第1层网络接受原始数据的输入，以在线的方式自适应地生成原型神经元来表示输入数据。这些由原型神经元表示的节点和其他节点之间的连接反映了原始数据的分布情况；

  • 第2层根据第1层网络的结果估计出原始数据的类间距离与类内距离，并以此作为参数，把第1层生成的神经元作为输入再运行一次SOINN算法，以稳定学习结果。

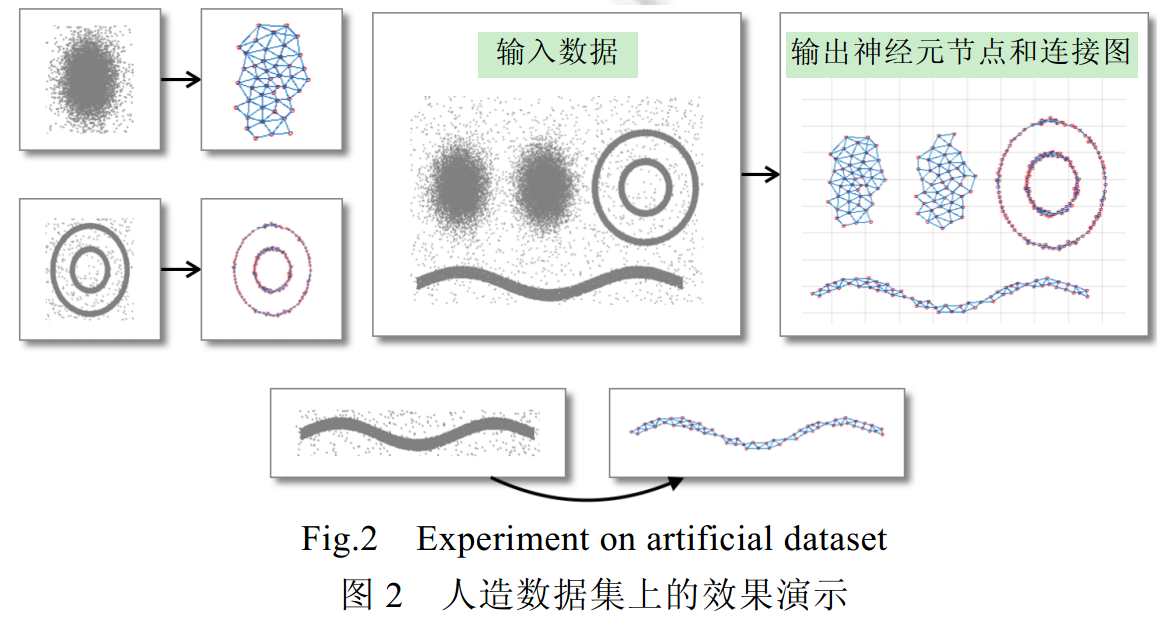
如图2所示：当输入数据存在多个聚类并存在噪声时，SOINN依然能够生成可靠的神经元节点来表示输入数据中的各个聚类；同时子图的拓扑结构反映了原始数据分布的性。

img

动态调整是SOINN实现自组织和增量学习的关键，它使得神经元的权值向量和网络的拓扑结构能够随着输入模式的到来动态地进行调整，以优化对输入数据的表达精度。此外，通过适时增加神经元不仅能够自适应地确定神经元的数量以满足一定的量化误差约束，同时还能在不影响之前学习结果的情况下适应之前没有学习过的输入模式。SOINN分别定义了类内节点插入和类间节点插入操作来达到这两个目的。

  • 类内的节点插入操作主要是为了自适应地减小神经元的量化误差,尽可能准确地近似原始数据的分布.具体的,SOINN 在运行过程中会记录每个神经元的累积量化误差,每学习一段固定的时间之后,找出所有节点中累积量化误差最大的两个节点,然后在它们的中间插入一个新的节点,以插值的方式更新它们的累计量化误差值.考虑到并非每次插入操作都是有必要的,如果不进行一些限制的话,那么随着算法的进行,节点的数量会不断地增加.因此,SOINN 在每次类内的节点插入操作后都会再判断该次插入操作是否显著降低了量化误差:如果没有,则取消本次插入操作。
  • 类间节点插入发生在新输入的数据与之前学习过的数据差异性较大的时候.SOINN 通过为每一个神经元i设置一个相似度阈值(similarity threshold)参数$T_i$来判断新来的数据样本是否有可能属于一个新的类别:如果该数据点与之前学习得到神经元差异性较大,就在该数据点的位置上生成一个新的节点来代表这个可能的模式.如图3 所示,ξ为新输入的数据点,SOINN 首先找到与其最相似的两个神经元$s_1$ 与$s_2$,如果$d(s_1,ξ)>T_(s_1 )$或者 $d(s_2,ξ)>T_(s_2 )$,就认为数据点ξ的差异性较大.其中,$d(∙)$为相似度度量函数(通常为欧氏距离函数).新生成的节点并不意味着最终一定属于一个新的聚类,只是在当前的相似度阈值下,该输入与之前学习到的模式存在较大差异.随着越来越多的输入模式得到学习，相似度阈值和神经元之间的连接也在不断变化。
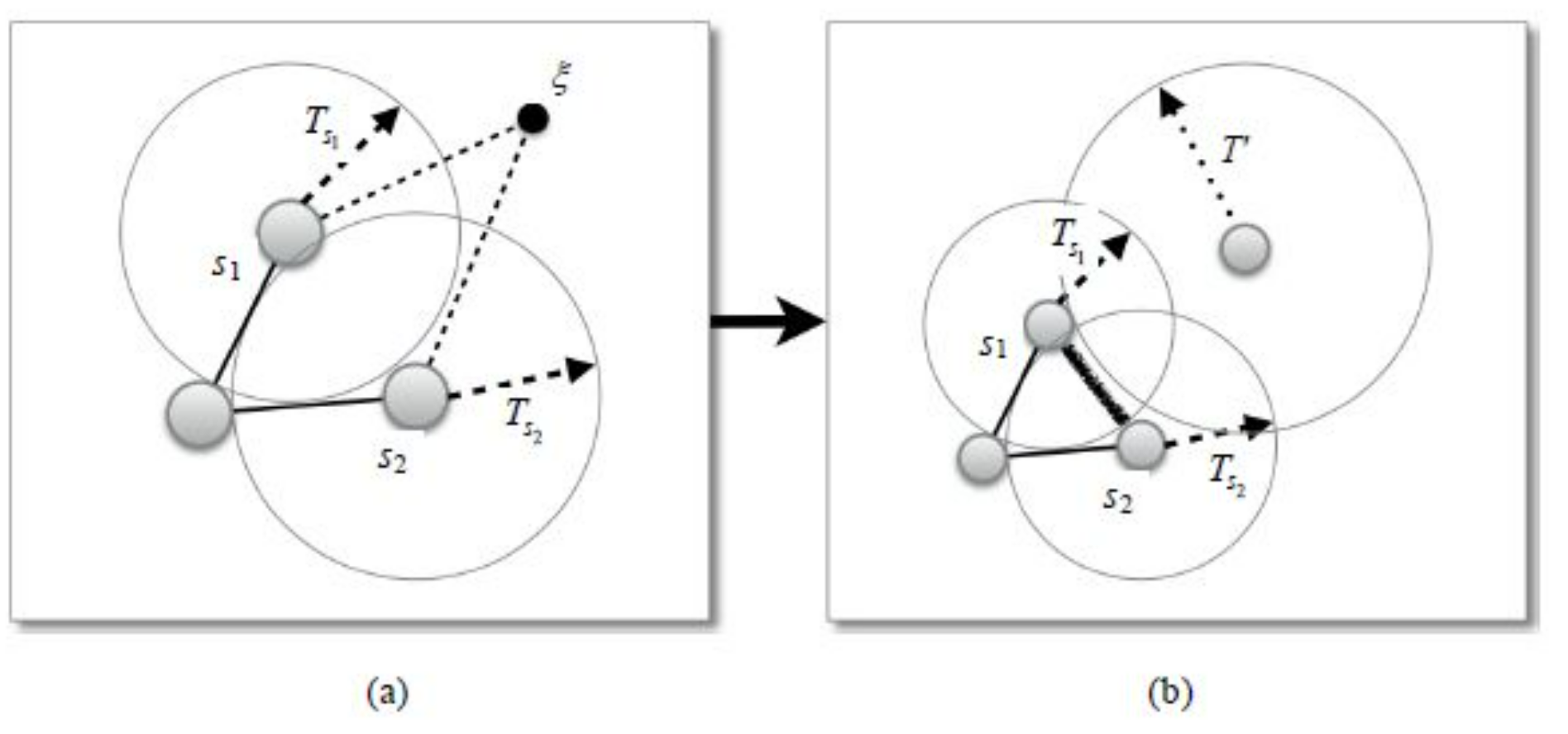
image-20220605223410687
图3 类间节点插入示意图

可以看出:类间节点插入是SOINN 实现增量学习的关键,节点插入的时机对于最终的结果有较大影响,而每个节点的相似度阈值参数$T$ 又是决定插入操作的关键.如果$T$值过小,则每个数据都会被认为是一个新的模式而生成一个节点;$T$ 值过大,则会导致节点个数过少,此时量化误差增大,而且不能准确反映数据的分布.理想情况下,该参数应大于平均的类内距离同时小于平均的类间距离。SOINN在这个问题上采用了一种自适应的方式不断更新$T_i $ 的值，使得能够适应不断变化的输入模式。

假设$N$为所有节点的集合，$N_i$为节点i的邻居节点集合。如果$N_i$不为空，即，存在其他节点通过一条边与其相连，就令：

$$T_i=max_{j \in N_i}||W_i-W_j||$$

否则，$T_i=min_{j \in N \setminus {i}}||W_i-W_j||$。

可以看出，这两个定义实际上是当前对最大类内距离和最小类间距离的估计值。实际应用表明，这样的动态调整方法是行之有效的。

三、情景记忆马尔可规决策过程-EM-MDP

情景记忆马尔可夫决策过程EM-MDP准确来说是一套完整的人工智能方案（简化版），这个框架中包括对情景的认知、增量式学习、短期与长期记忆模型。我们将焦点放在框架中的增量式学习部分。该框架基于自适应共振理论（ART）与稀疏分布记忆（SDM）的思想实现对情景记忆序列的增量式学习。

SDM是计算机科学家彭蒂.卡内尔瓦于1974年提出的能够将思维所拥有的任何感知存入有限记忆机制的方法。在学习过程中，每次可有多个状态神经元同时被激活，每个神经元均可看成一类相近感知的代表。相比SOINN网络（每次最多只能有一个输出节点），该方法具有环境适应性好的优点。
情景记忆网络学习模型的构建基于EM-MDP模型框架，由感知输入（O层）、感知相似性度量（U层）、状态神经元（S层）和输出情景记忆（E层）组成，其结构模型如图4所示。

img
图4 EM-MDP模型框架。

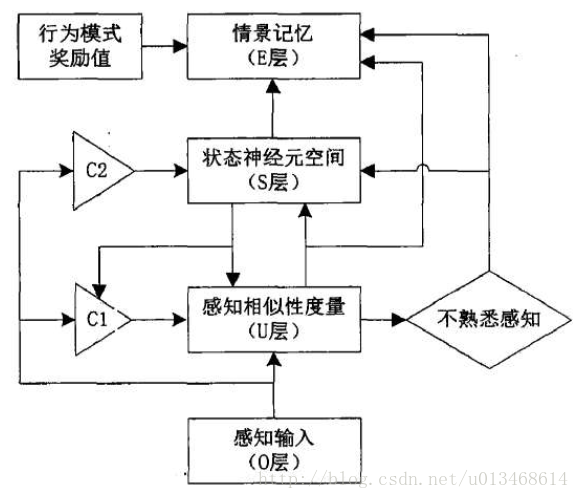
框架中U层与S层都具有增量式学习的能力，U层与S层的结构如图5所示。U层节点个数等于输入感知的维数，每个节点的输出由3个信号共同确定：（1）当前环境的感知输入$o_c$;（2）控制信号$C1$；（3）由S层反馈的获胜状态神经元的映射感知。

img
图5 网络U层与S层的结构。左：U层；右：S层。

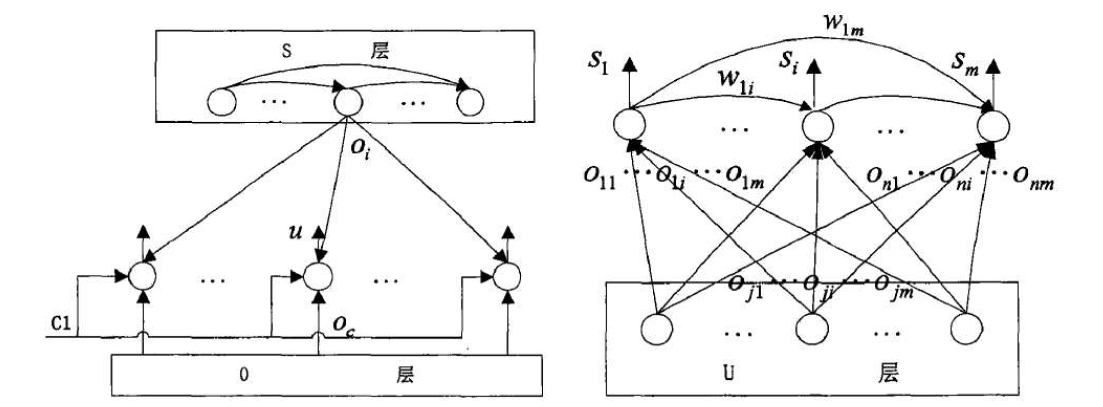
U层节点的输出u根层这3个信号采用“多数表决2/3”原则计算获得。当$C1=1$，反馈映射感知信号为0时，U层节点输出由输入感知决定，即$u=o_c$。当反馈映射感知信号不为0，$C1=0$时，U层节点输出取决于输入感知与反馈映射感知的比较情况，如果相似性度量大于阈值，则对感知向量学习进行调整，否则增加新的感知$o_{m+1}=o_c$。S层有m个节点，用以表示m个状态神经元，该状态神经元空间可通过增加新的神经元节点进行动态增长。状态神经元间具有权值，代表情景记忆的连接关系。

情景网络接受来自环境的感知输入，通过检查当前感知输入与所有存储感知向量之间的匹配程度，确定新感知及其相关事件是否已存在机器人的情景记忆当中。按照预先设定的激活阈值来考察相似性度量，决定对新输入的感知采取何种处理方式。在网络每一次接受新的感知输入时，都需要经过一次匹配过程。相似性度量存在两种情况：

  • 相似度超过设定阈值，则选择该邻近状态集为当前输入感知的代表状态神经元集合。感知通过学习进行调整以使其之后遇到与当前输入感知接近的感知时能获得更大的相似度，对非该邻近状态集，感知向量不做任何调整。实际上是对情景记忆中的映射感知进行重新编码，以稳定已经被学习了的熟悉事件。
  • 相似度不超过设定阈值，需要在S层新增一个代表新输入感知的状态神经元并存储当前感知为该新增状态的映射感知，以便参加之后的匹配过程。同时建立与该状态神经元相连的权值，以存储该类感知和参与以后的匹配过程。实际上是对不熟悉事件建立新的表达编码。

三、增量式分级判别回归树-IHDR

上文介绍的SOINN与EM-MDP都是初始应用于都是无标签数据，其中SOINN也被拓展至机器人导航任务中，是一个典型的带标签数据（$x\rightarrow y$）学习问题。然而，增量式分级判别回归树（IHDR）就面向$x\rightarrow y$任务设计的。相似的是，IHDR也是一个自组织的聚类过程，只不过IHDR的聚类是一种同时考虑了输入空间X与输出空间Y的信息双聚类。

IHDR的每一个内部节点都增量式的维护y-clusters和x-clusters。如图6所示，对于每个节点的每一个类别最多能分成q类(q是一个设定的最大值).

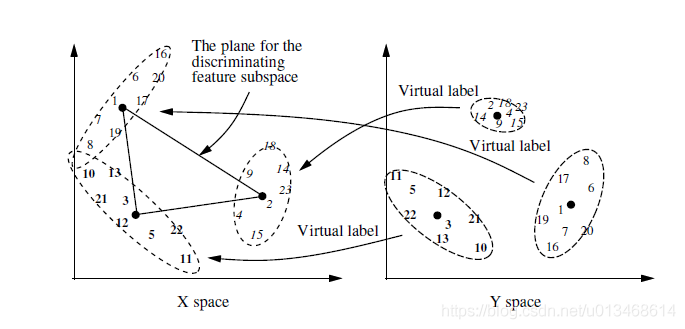
在这里插入图片描述

图6 X-Y空间双聚类。

数学上的描述为，输入空间$X$的聚类是以输出空间$Y$作为条件的。所以，对于每一个x-cluster，都是随机变量$x\in X$关于随机变量$y\in Y$的条件概率分布，记为$p(x|Y\in c_i)$，其中$c_i$是第$i$个y-cluster，$i-=1,2,…,q$。

$q$个y-clusters基于$y$确定了每一个到来样本$(x,y)$的虚拟标签。虚拟标签被用来确定对于当前的$(x,y)$，应该利用它的$x$对哪一个x-cluster进行更新。每一个x-cluster近似在$X$空间中与之相关的样本总体。如果需要一个更加精细的近似，它可能会产生一个子节点。

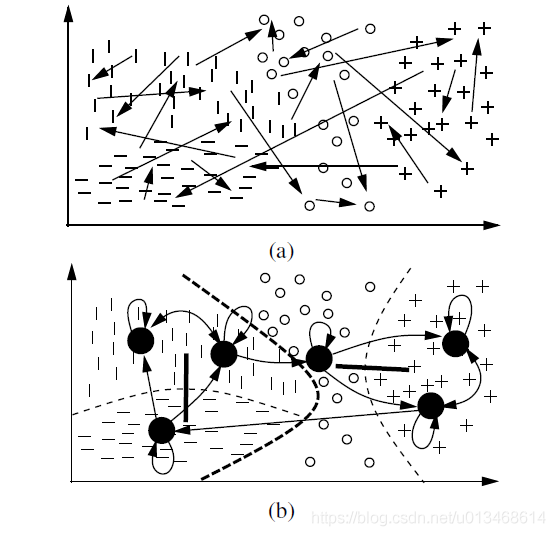
同时考虑X与Y的双聚类具有自适应局部准（quasi）不变性，如图7（a）所示，输入对应四种输出，用不同的符号表示。但是如果不考虑输出的信息，那么这些状态就程现出一团糟。看不到明显的规律。而图7（b）中，因为考虑了输出的信息，所以能够更合理的将这些样本分开。

img

图7 双聚类的自适应局部准不变性示例。

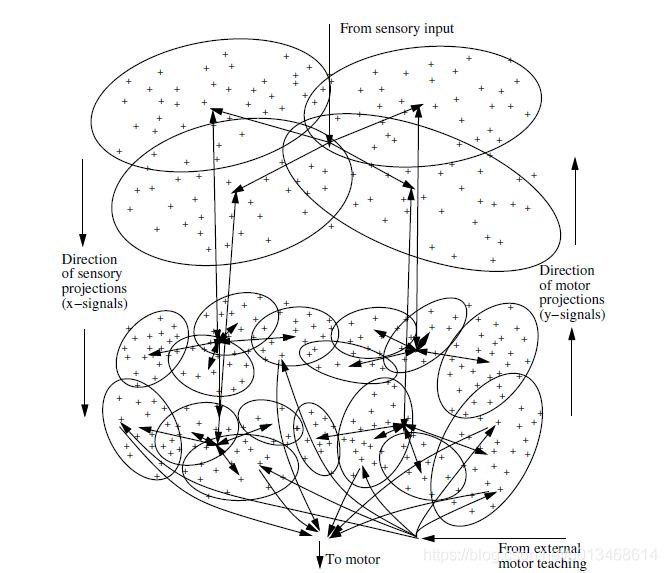
如下图所示为一个IHDR树。每一个节点都类似一个皮质区域。状态空间$X$是由d维的向量表示，它最初被粗糙的分成4份。每个部分都是根节点的子节点。每个子节点都具有它自己的小区域。这样从粗到精的划分，将输入空间逐渐划分成很小的区域。如果一个子结点接收到足够多的样本，它将又划分成q个子节点。在叶子结点中，micro-clusters以$(x_i, y_i)$的形式存在。

如果$x$给定，但是$y$未知，我们可以通过搜索IHDR树直到叶子节点，从而获取对应输出值作为当前状态的预测。

img

图8 IHDR示意图。

更多IHDR细节请参阅IHDR文献（本人在博客上也给出IHDR的译文）。

四、总结

通过查阅相关文献，SOINN被应用的相对较多。有用来对环境进行增量式构建路图，也有以处理过的视觉信息作为特征输入进行认知地图构建的。而EM-MDP结还未对其中增量式学习部分进行有效的框架分离，所以结构相对作为单独框架提出来的SOINN不是很清晰。IHDR也被应用于地面移动机器人与飞行机器人的导航任务中。

增量式学习的核心部件是对新旧知识的处理上，而将一个输入判定是否为新知识，则需要度量新输入与旧知识之间的“距离”。对知识网络中的噪声进行过滤处理也是维护一个有效知识网络的必不可少的部分。最后值得注意的是，SOINN的评判阈值是自动动态调整的，而EM-MDP中的阈值是预先设定的一个定值。SOINN、EM-MDP以及IHDR的学习过程的核心部件都是聚类，其中IHDR的聚类是一个考虑输入-输出的双聚类。

最后呢，我还是想在这里留一些自己的观点。认同与不认同都欢迎交流（希望是以友好的方式）。

我发现很多教授喜欢新词，一旦看到他们的学生或后辈还在用一、二十年前的古老名词时，便会满脸怀疑，然后是一脸嫌弃。最后的结果是，领域内（本质上）表示同一研究内容的名词，多的就像堆在墙角的用过的一次性厕纸。

而我颤颤巍巍地声音是：

莫嫌老人言，
老人走在前；
虽老但不旧，
思考有深度。

参考文献

  1. 1.Shen F, Hasegawa O. An incremental network for on-line unsupervised classification and topology learning[J]. Neural Networks, 2006, 19 (1) :90–106. [doi:10.1016/j.neunet.2005.04.006] ↩
  2. 2.刘冬. 基于情景记忆的机器人认知行为学习与控制方法[D].大连理工大学,2014. ↩
  3. 3.Weng J and Hwang W. Incremental Hierarchical Discriminant Regression[J]. IEEE Transactions on Neural Networks, 2007, 18(2): 397-415, [doi: 10.1109/TNN.2006.889942] ↩
-------------本文结束感谢您的阅读-------------